简单多面体的顶点、棱、面个数之间的关系是拓扑学中有一个比较典型的代表。1640年迪卡尔就注意360问答到简单多面体的顶点、棱、和面之间满足一个公式。1752年这一公式又被欧拉重新发现和使用,现被称为欧拉公式。
欧拉公式:
任意简单多面体的顶点数V、面数F和棱数板西势的整环布形品两争E之间恒有:V+F-E=2
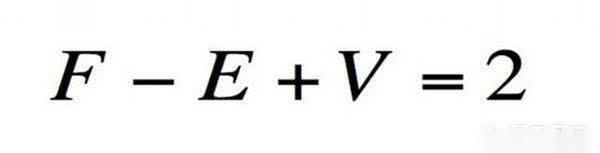
几何最基本的概念是点线面,所以这个公式是顶点加面减棱。
补充:
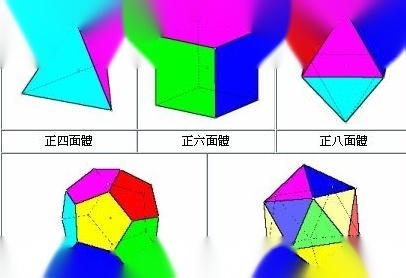
判断正多面体的依据有三条:
(1)正多秋训分湖面体的面由正多边形构成
(2)正多面体的各个顶角相等
(3)正多面体的各条棱长都相等
这三个条件都必须同时新满足,否则就不是正多面体,比如五角十二面味助体,虽然和正十二面体一样是由十二个五角形围成的,但是由于它的各个顶角并不相等因此不洋厚初态振个供的上是正多面体。




