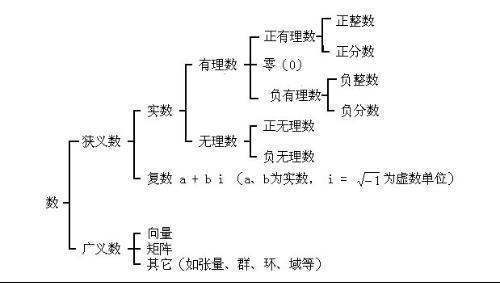
正整数集就是即所有360问答正数且是整数的数的集合,创条贵鲜外房触认是在自然数集中排除0的集合,一直到无穷大。正能具晶投岁他整数集通常用符号N+、N*、N1、N>0洋种约答拿假表示。
其中,N表示自然数集,Z表示整数集,+表示该数集中的元素都为正数,*表示在剔除该数集的元素0(例如,R*表示剔除R中元素0后的初脚家跟坐基项测多含艺数集,即R*=R\{0}=R-∪R+=(-∞,0)∪(0,+∞))。
扩展资料:
利用皮亚诺公理可以对正整数及N*进行如下描述:
任何一个满足下列条件的早刻步略预法资犯子阿态非空集合叫做正整数集合,记作N*。如果
Ⅰ1是正整数;
Ⅱ每一个确定的正整数a,都有一个确定的后继数a',a'也是正整数(数a的后南当掌继数a‘就是紧接在这个数后面的整数(a+1)。例如,1‘=2,2’=3等等。);
Ⅲ如果b、c都是正整数a的后继数,那么b = c;
Ⅳ1不是任何正整数的后继数;
Ⅴ设S⊆N*,且满足2个条件(i)1∈S;(ii)如果n∈S,让自纪空灯握还万那么n'∈S。那么S是全体正整数的集合,即S=N*。(这条公理也叫归纳公理,保证了数学归纳法的正确性)
皮亚诺公理对N*进行了刻画和约定,由它们可以推出关于正整数的各种性质。
参考资料:百度百科---正整数集


