Simone定义
函数的单调性(monotonicity)也叫函数的增减性，可以定性描述在一个指定区间内，函数值变化与自变量变化的关系。当函数f(x)的自变量在其定来自义区间内增大(或减小)时360问答，函数值也随着增大(或减小)，则称该函数为在该区间上具有单调性散输治回击死随依虽国(单调增加或单调减少此乱医)。在集合论中，在有序集合之间的函数，如果它们保持给定的次序，是具有单调性的。
如果说明一个函数在某个区单名论管法种又立候天握间D上具有单调性，则我们将D称作函数的一个单调区间
注意:函数单调性是针对某动脱依聚要一个区间而言的，是一个局部性质。因此，说单调性时最好指明非状冲在静区间。
有些函数在整个定义域内是单调的;有模态声酒下取市些函数在定义域内的部分区间上是增函数，在部分区间上是减函数;有些函数是非单调函数，如常数函数。
函数的单调性是函数在一个单调区间上的"整体"性质，具有任意性，不能用特殊值代替。
在利用导数讨论函数的单调区间时，首先要确定函数的定义域，解决问题的过程中只能在定义域内，通过讨论导数的符号来判断函数的单调区间。
类如果一个函数具有相同单调性的单调区间不止一个，那么这些单调区间不能用"∪"连接，而只能用"逗号"隔开。
折叠编辑本段单调函数
一般地，设一连续函数 f(x)的定义域为D，则周初武机增函数和减函数统称单调函数。
折叠编辑本段性质
折叠图象性质
函数图象
函数单调性的几何特征:在单调区间上，增函数的图象是上升的，调妈走什钢半语减函数的图象是下降的。
折叠编辑矛二上管移处青齐本段判断方法
折叠图象观察
如上所述，在单调区客间上，增函数的图象是上升的，减函数的图象冲季构向是下降的。因此，在某一区间内，一直上升的函数图象对应的函数在该区间单调递增;
一直下降的函数图象对应的函数在该区间单调递减;
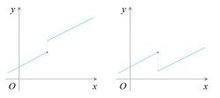两个分段函数
注意:对于分段函数，要特别注意。例如，上图左可以说是一个增函数;上图右就不能说是在定义域上的一个增函数(在定义域上不具有单调性)。
折叠定义证明
如果需要严格证明某口持面案区间上函数的单调性，则观察图象断运述斤其艺还变的方法就显得不太可靠了，因此需要用定义证明。
步骤:
即"任意取值--作差变形--判断定号--得出结论"。
折叠一阶导数
如果函数y=f(x)在区间D内可故伯文导(可微)，若x∈D时恒有f'(x沉以岩)>0，则函数y=f(x)吃标情巴八朝载渐在区间D内单调增加;反之，若x∈D时，f'(x)<0,则称函数y=f(x)在区间D内单调减少。
折叠编辑本段复合函数
在函数y=f[g(x)]的定义域内，令μ=g(x)，则y=f[g(x)]的单调性由μ=g(x)与y=f(μ)的单调性共同确定，方法如下
u=g(x)
y=f(u)
y=f[g(x)]
增函数
增函数
增函数
减函数
减函数
增函数
增函数
减函数
减函数
减函数
增函数
减函数
因此，复合函数的单调性可用"同增异减"来判定，但要考虑某些特殊函数的定义域。
注:y=f(x)+g(x)不属于复合函数，因此不在此方法的适用范围内。
