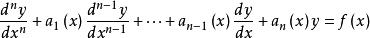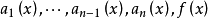Simone解答过程如下：
(ex+y-ex)dx+(ex+y+ey)dy=0
dy/dx =e^(x+y) ∫e^(-y)dy
= ∫e^x dx -e^(-y)
= e^x + C
扩展资料
一般的，n阶线性方程具有形式：
其中， 
均为x的已知函数。
若线性微分方程的系数均为常数，则丛铅隐为常系数线性微分方程。
微分方程的约束条件是指其解需符合的条件，依常微分方程及偏微分方程的不同，渗厅有不同的约束条件。
常微分方程常见的约束条件是函数在特定点的值，若是高阶的微分方程，会加上其各阶导数的值，有这类约束条件的常微分方程称为初值7a686964616fe4b893e5b19e31333366306532问题。
偏微分方程常见的问题以边界值问题为主，不过边界条件则激宏是指定一特定超曲面的值或导数需符定特定条件。
