方差分析的基本原理是认为不同处理组的均数间的差别基本来源。总偏差平方和 SSt = SSb + SSw。
组内SSw、组间SSb除以各自的自由雹升度(组内dfw =n-m,组间dfb=m-1,其中n为样本总数,m为组数),得到其均方MSw和MSb,一种情况是处理没有作用,即各组样本均来自同一总体,MSb/MSw≈1。
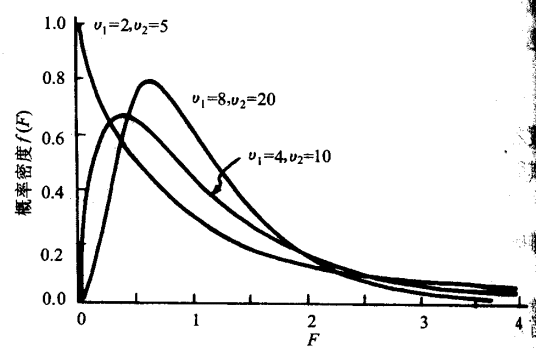
另一种情况是处理确实有作用,组间均方是由于误差与不同处理共同导致的结果,即各样本来自不同总体。那么,MSb>>MSw(远远大于)。MSb/MSw比值构成F分布。用F值与其临界值比较,推断各样本是否来自相同的总体。
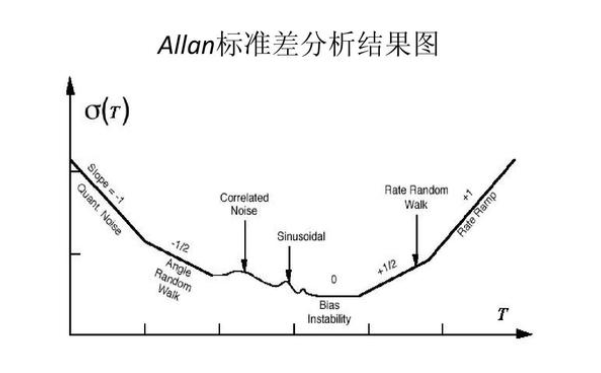
扩展资料:
在方差分析中,我们把要考察其均值是否存在显著差异的指标变量称为响应变量,对响应变量取值有影响的其他变量称为因素。
例如,信用卡消费水平和治疗效果为响应变量,地区和药品则为因素。在方差分析中,因素的取值应为离散型的,其不同的取值称为水平。
根据模型的自由度(s-1)以及误差自由做乎度的自由度(n-s),可以确定一个F分布。由该F分布的概率密度函数和F0,可以进一步计算出在该F分布中大于F0的源胡老p值,p=pr(x>F0)。
参考资料来源:百度百科-方差分析