秦九韶算法是中国搜睁雀南宋时期的数学家秦九韶提出的一种多项式简化算法。在西方被称作霍纳算法。
秦九韶算法是一种将一元n次多项式的求值问题转世早化为n个一次式的算法。其大大简化了计算过程,即使在现代,利用计算机解决多项式的求值问题时,秦九韶算法依然是最优的算法。
一般地,一元n次多项式的求值需要经过[n(n+1)]/2次乘法和n次加早胡法,而秦九韶算法只需要n次乘法和n次加法。在人工计算时,一次大大简化了运算过程。
把一个n次多项式f(x)=a[n]x^n+a[n-1]x^(n-1)+......+a[1]x+a[0]改写成如下形式
f(x)=a[n]x^n+a[n-1]x^(n-1))+......+a[1]x+a[0]
=(a[n]x^(n-1)+a[n-1]x^(n-2)+......+a[1])x+a[0]
=((a[n]x^(n-2)+a[n-1]x^(n-3)+......+a[2])x+a[1])x+a[0]
=......
=(......((a[n]x+a[n-1])x+a[n-2])x+......+a[1])x+a[0].
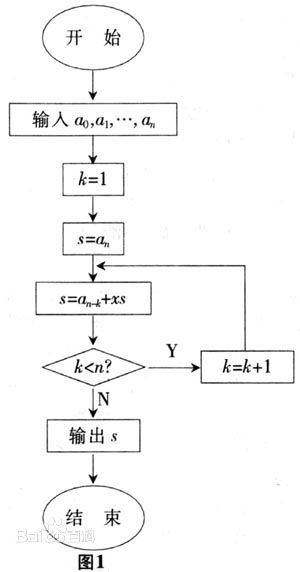
求多项式的值时,首先计算最内层括号内一次多项式的值,即 v[1]=a[n]x+a[n-1] 然后由内向外逐层计算一次多项式的值,即
v[2]=v[1]x+a[n-2]
v[3]=v[2]x+a[n-3]
......
v[n]=v[n-1]x+a[0]
这样,求n次多项式f(x)的值就转化为求n个一次多项式的值。(注:中括号里的数表示下标)
结论:对于一个n次多项式,至多做n次乘法和n次加法。




