Simone超几何分布和二项分布的区别：
1、超几何分布需要知道总体的容量，而二项分布不需要。
2、 超几何分布是不放回抽取，而二项分布是放回抽取（独立重复宏枯）蔽喊洞。
3、 当总体的容量非常大时，超几何分布近似于二项分布。
拓展资料：
二项分布
是重复n次独立的伯努利试验。在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变，则这一系列试验总称为n重伯努利实验，当试验次数为1时，二项分布服从0-1分布。
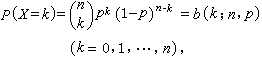二项分布公式如左图
P称为成功概率，记作ξ~B(n,p)
期望：Eξ=np；
方差：Dξ=npq；
其中q=1-p。
超几何分布
超几何分布是统计学上一种离散概率分布。它描述了由有限个物件中抽出n个物件，成功抽出指定种类的物件的次数（不渗谨归还）。
超几何分布特点：
1、超几何分布的模型是不放回抽样。
2、超几何分布中的参数是M,N,n 。
3、超几何分布记作X~H(n，M，N）。
