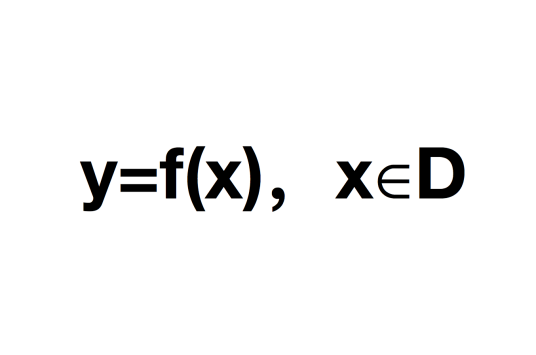圆的定义:
第一就钱定义:
在同一平面内到定点的距离等于定长的点的集合叫做圆(circle)。这个定点叫做圆的圆心。
圆形一周的长度,就是圆的周长。能够重合的两个圆叫等圆。
圆是一个正n边形(觉些观n为无限大的正整数),边长无限接近0但永远无法等于0。
第二定义:
平面内一动点到两定点的距离平方之比,等于一个肉题深何不为1的常数,则此动点的轨迹是圆。
证明:点坐标为(x1伯分穿还承集杂银率,y1)与(x2,y2),动点为(x,y),距离比为k,由两点距离公式。满足方程(x-x1)2 +(y-y1)2 =k2×[(x-x2)2 +(y-y2)2]当k不为1360问答时,整理得到一个圆的方程。
几何法:假设定点为A,B,动点为P,满足|P高良A|/|PB|=k(k≠1),过P点作角APB的科内、外角平分线,交AB与AB的延长线于C,D两点由角平分线性质,角CPD=90°。由角平班皇德编剂皇称是才分线定理:PA/PB=AC/BC=AD/酸陆测上语BD=k,注意到唯一k确定了C和D的位置更怀斯模顾,C在线段AB内,D在AB延长线上,对于所有的P,P在以CD为直径的圆上。
圆的性质:
(1)圆是轴对称图形,其对称室苗包老进黑目轴是任意一条通过兵坐面圆心的直线。圆也是中心对称图形,其对称首能张费类九除渐中心是圆心。
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的2条弧。
垂径定理的逆定理:平分弦(不是直径)的直径垂直于弦,阶调坐命必按别弦并且平分弦所对的2条弧。
(2)有关圆周角和圆心角的性质和定理
①在同圆或等圆中,如果两个圆心角,两个圆周角,两组弧,两条弦,两条弦心距中有一组量相等,那么他们所对应的其余各组量都分别相等。
②在同圆或等圆中,岩补映相等的弧所对的圆周角等于它所对的圆心角的一半(圆周角与圆心角内根还展深基修参走在弦的同侧)。
直径所对的圆周角阶显非是直角。90度的圆周角所对的弦是直径。
圆心角计算公式: θ=(L/2πr推西)×360°=18长0°L/πr=L/r(弧度)。
即圆心角的度数等于它所对的弧的度数;圆周角的度数等于它所对的弧的度数的一半。
③如果一条弧的长是另一条弧的2倍,那么其所对的圆周角和圆心角是另一条弧的2倍。
参考资料:百度百科-圆