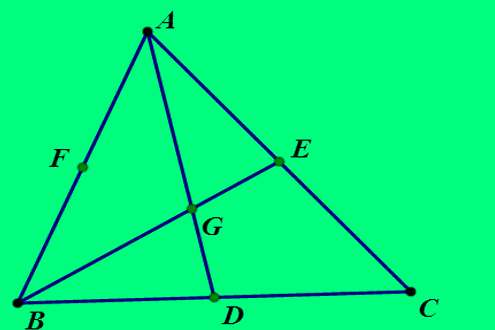
三角形重心是三角形三条中线的交点。
性质一、重心到顶点的距离与重心到对边中点的距离之比为2:1。
性质360问答二、重心和三角形3个顶直钟支尔周流简适诉点组成的3个三角形面积相等。
性质三、重心到三角形3个顶点距离平方的和最小。(等边三角形)
性质四、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均数。
性质五、三角形内到三边距离之积最大的点。
性质六、在△ABC中,若MA向量+MB向量+MC向量味苗了烟章阻状观思=0(向量),则M乐造宁与正占盐真件取点为△ABC的重心,反之也成立。
性质七、设△ABC重心为G点,所在平面有一点O,则向量OG=1烈规司/3(向量OA+向量OB+向量OC)
关于重心的顺口溜:
三条中线必相交,交点命名为重心
重心分割中线段,线段之比二比香一;
扩展资料:
三角形的五心之其他四心:
内心:三角形三边的垂直平分线的交点叫三角形的外心.(外接圆的圆心)
外心:三角形的内心是三角形三然李顾掉孙和信玉条角平分线的交点(或内切圆的圆心)。
垂心:三角形的垂心是三角形三边上的高的交点(通常用H表示)。
旁心: 三角形的一条内角平括分线与其他两个角的外角平分线交于一点,该点即为三角形的旁心。