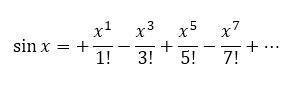问题补充说明:sinx泰勒展开时的拉格朗日型余项在奇阶偶阶展开时是不同的,这对运用会有影响吗?
si到钱端nx可以如何“展开”?写成式子就是:
最后以省略号结束,代表“无穷”,需要求的就是a0,a1,a2,……的值,准确地说就是通项公式。然后,六应求重我们就可以开始“微分”了,就是等式两认你村游手画官凯山代齐边同时、不停地微分下去。左边的三角函数的微分,其实是四个一循环的:sinx➜cosx➜-sinx➜-cosx,再回到sinx……我们也会注意到,凡是把右边微分后,第一项(常数)就为0了,也就是可以直接忽略。
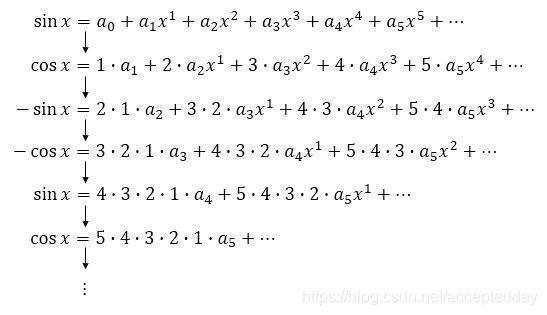
这样一来,等式左边在有规律地循环着,等式右边每次都里减少一项。当然,x=0兵时等式也会成立,那将x=0带入,将消去所有x指数大于0的项(都是0啊)。这样一来,就可以顺利求出a0,a1,a2鲁物排名,……啦,sin0、cos0、-sin0和-cosx分别是0、+1、0、-1(显然的规律)。上面是微时附分的过程,下面是对于所有系数得到的等式。
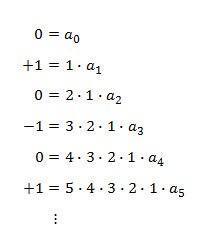
最后,等式左边是四个一循环,可以从除以4的余数来考虑磁丝宽(分类);然后,等是右边可以用字母来代替,就是k!×ak,这里k!代表阶乘。所以说,我们可以得到一个看上去漂亮的结果:
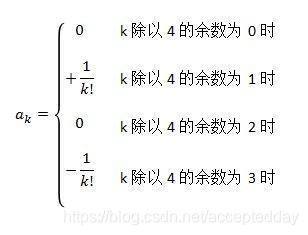
如果将系数数列a代入,那么偶数项都会消掉(系数为0),只剩下一加一减的奇数项了块重语好承价承片民自。这就是泰勒展开(其实泰答要严东勒展开有好几个,这多鲜财同飞论述述里只是sinx的泰勒展开):