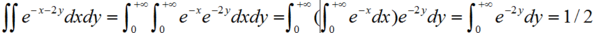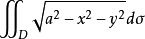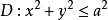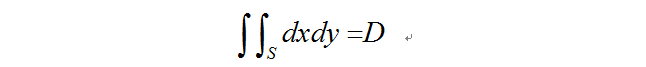Simone把二重积分化成二次积分，也就是把其中一个变量大森当成常量比如Y，然后只对一个变量积分，得到一个只含Y的被积函数，再对Y积分就行了。
题目积分区域中，x,y并不成函数关系，要是积分区域是由比如说1<=x<=2,y=f(x),y=g(x),所围成的话，那么就要先对y积分其中上下限就是f(x),g(x),要看谁的图形在上谁就是上限，这时候的x就当做一个常数来看待（只含有x的项可以像提出常数一样提到积分号外面来）。
这个第一次积分得到一个关于x的函数（这个结果是第二次积分的表达式），然后再对x积分，这时候上下限就是2和1。这样就得到积分值了。
扩展资料：
几何意义
在空间直角坐标系中，二重积分是各部分区域上柱体体积的代数和，在xoy平面上方的取正，在xoy平面下方的取负。某些特殊的被积函数f（x，滚汪亩y）的所表示的曲面和D底面所为围的曲顶柱体的体积公式已知，可以用二重积分的几何意义的来计算。
例如二重积分
陵埋
其中
表示的是以上半球面为顶，半径为a的圆为底面的一个曲顶柱体，这个二重积分即为半球体的体积
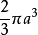参考资料：百度百科-二重积分
