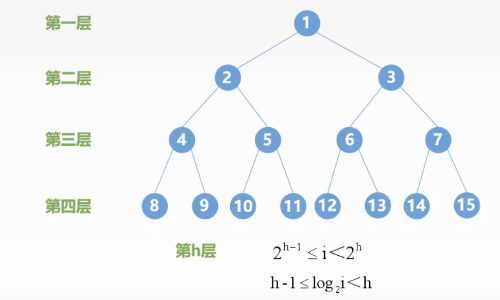
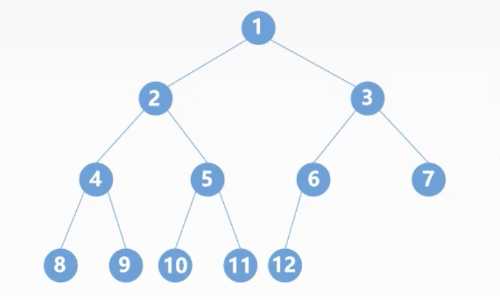
满二叉树和完全二叉树的区别图解,如下所示:
完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与码孝顷轿深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
对于满二叉树,除最后一层无任何子节点外,每一层上的所有结点都有两个子结点二叉树。而完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
满二叉树定义:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉迟乎稿树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。
完全二叉树定义:若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。