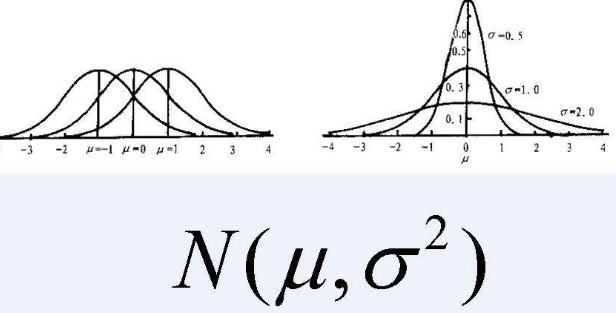SS即离差平方和,各项与平均项之差的平方的总和。定义是设x是一个随机变量,令η=x-Ex, 则称η为x的离差,它反映了x与其数学期望Ex的偏离程度。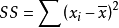
根据数学期望的性质,离差的数学期望总是等于0,没有实用价值
通常用随机变量x离差的平方的数学期望来描述随机变量旁此x的分布的分散程度,并把其称为x的方差,记作Dx
总体方差D(x)=SS/n,样本方差D(x)=SS(n-1)。
扩展资料
方差分析的基本原理是认为不同处理组的均数间的差别基本来源有两个:
1、实验条件,郑启握即不同的处理造成的差异,称为组间差异。用变量在各组的均值与总均值之偏差平方和的总和表示,记作SSb,组间自由度dfb。
2、随机误差,如测量误差造成的差异或个体间的差异,称为组内差异,用变量在各组的均值与该组内变量值之偏差平方和的总和表示, 记作SSw,组内自由度dfw。
总偏差平方和SSt=SSb+SSw。
组内SSw、组间SSb除以各自的自由度(组内dfw=n-m,组间dfb=m-1,其中n为样本总数,m为组数),得到其均方MSw和MSb,一种情况是处理没有作用,即各组样本均来自同一总体,MSb/MSw≈1。
另一种情况是处理确实有作用,组间均方是由于误差与不同处理共同导致的结果,即各样本来自不同总体。那么,MSb>MSw(远远大于)。
MSb/MSw比值构成F分布。用F值与其临界值比较,推断各样本是否来自相同的总体。
参考资料喊庆来源:百度百科-方差分析
参考资料来源:百度百科-离差平方和